Nelder–Mead method

In the previous subsection, the gradient methods require the objective function to be once or twice continously differentiable.

The Nelder–Mead method [NM65] described in this subsection, requires the objective function to be continous only. Therefore it is an example of a derivative-free optimization method.

This method is implemented in the Matlab/Octave function fminsearch. See [LRWW98] and [PCB02] for modifications and references.

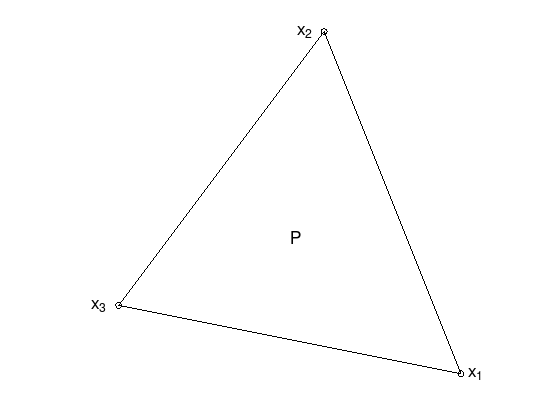
Basic concept of this method is a simplex (polyhedron), here defined as a set of \(n + 1\) linear independent points \(P = \{ x_1, x_2, \ldots, x_{n + 1} \} \subset \mathbb{R}^{n}\) (the vertices of the simplex).

In geometry the convex hull of \(P\) is usually defined as simplex. For dimension \(n = 2\), the simplex is a non-degenerate triangle, as in the following figure. For dimension \(n = 3\), a non-degenerate tetrahedron.

x1 = [ 0.0, 0.0];
x2 = [-0.4, 1.0];
x3 = [-1.0, 0.2];
x = [x1; x2; x3; x1];
x_label = {'x_1', 'x_2', 'x_3'};
plot (x(:,1), x(:,2), 'ko-');
hold on;

tprops = {'FontSize', 18};
for i = 1:3
  if (x(i,1) < 0)
    x_offset = -0.08;
  else
    x_offset = 0.02;
  end
  text (x(i,1) + x_offset, x(i,2), x_label{i}, tprops{:});
end

text (-0.5, 0.4, 'P', tprops{:});
axis equal;
axis off;

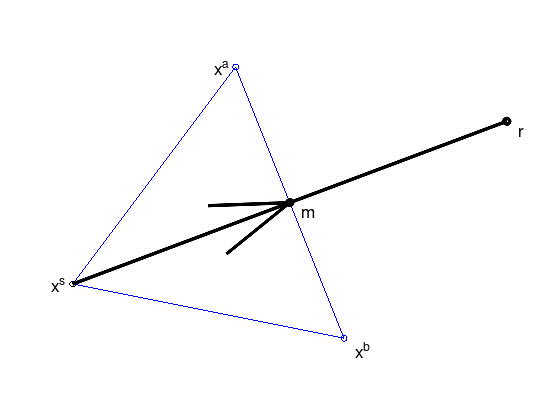
Iteration step of the simplex method (\(n \geq 2\))

1. Compute the following indices \(s, a, b \in \{ 1, \ldots, n + 1 \}\):

   • \(x^{s} := \operatorname{argmax} \{ f(x) \colon x \in P \}\) (worst point)

   • \(x^{a} := \operatorname{argmax} \{ f(x) \colon x \in P, a \neq s \}\) (second worst point)

   • \(x^{b} := \operatorname{argmin} \{ f(x) \colon x \in P, b \neq s, b \neq a \}\) (best point)

1. Compute the centroid \(m\) of the \(n\) best points

   \[\begin{split} m := \frac{1}{n} \sum_{\substack{i = 0 \\ i \neq s}}^{n + 1} x^i, \end{split}\]

   and the point \(r\) reflected at the center \(m\)

   \[ r := m + \alpha (m - x^s), \]

   with \(\alpha = 1\).

function plot_line (points, LineSpec)
  plot (points(:,1), points(:,2), LineSpec{:});
end

function plot_triangle (points, LineSpec)
  % Repeat first point.
  plot_line ([points; points(1,:)], LineSpec);  
end

xb = [ 0.0, 0.0];
xa = [-0.4, 1.0];
xs = [-1.0, 0.2];
m = xb + 0.5 * (xa - xb);
r = m  +        (m - xs);

points = [xb; xa; xs; m; r];
plabel = {'x^b', 'x^a', 'x^s', 'm', 'r'};

plot_triangle ([xb; xa; xs], {'bo-'});
hold on;
quiver (xs(1), xs(2), m(1) - xs(1), m(2) - xs(2), 'ko-', 'LineWidth', 4);
plot_line ([r ; m], {'ko-', 'LineWidth', 4});

tprops = {'FontSize', 18};
for i = 1:length (plabel)
  if (points(i,1) < -0.3)
    x_offset = -0.08;
    y_offset = 0.0;
  else
    x_offset = 0.04;
    y_offset = -0.04;
  end
  text (points(i,1) + x_offset, points(i,2) + y_offset, plabel{i}, tprops{:});
end

axis equal;
axis off;

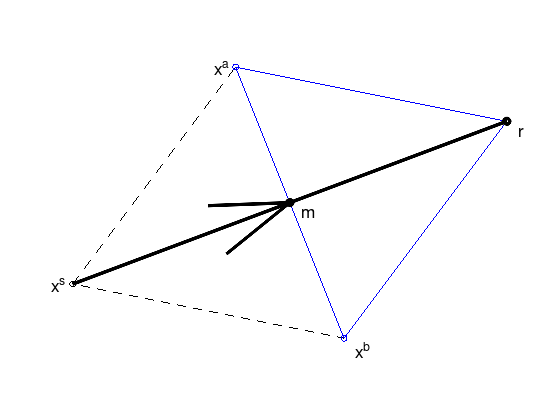
Case 1: Reflect

“New point is good.”

Replace \(x^s\) by \(r\), if \(f(x^b) \leq f(r) \leq f(x^a)\) and case 2 does not apply.

function plot_line (points, LineSpec)
  plot (points(:,1), points(:,2), LineSpec{:});
end

function plot_triangle (points, LineSpec)
  % Repeat first point.
  plot_line ([points; points(1,:)], LineSpec);  
end

xb = [ 0.0, 0.0];
xa = [-0.4, 1.0];
xs = [-1.0, 0.2];
m = xb + 0.5 * (xa - xb);
r = m  +        (m - xs);

points = [xb; xa; xs; m; r];
plabel = {'x^b', 'x^a', 'x^s', 'm', 'r'};

plot_triangle ([xb; xa; xs], {'ko--'});
hold on;
plot_triangle ([xb; xa; r] , {'bo-'});
quiver (xs(1), xs(2), m(1) - xs(1), m(2) - xs(2), 'ko-', 'LineWidth', 4);
plot_line ([r ; m], {'ko-', 'LineWidth', 4});

tprops = {'FontSize', 18};
for i = 1:length (plabel)
  if (points(i,1) < -0.3)
    x_offset = -0.08;
    y_offset = 0.0;
  else
    x_offset = 0.04;
    y_offset = -0.04;
  end
  text (points(i,1) + x_offset, points(i,2) + y_offset, plabel{i}, tprops{:});
end

axis equal;
axis off;

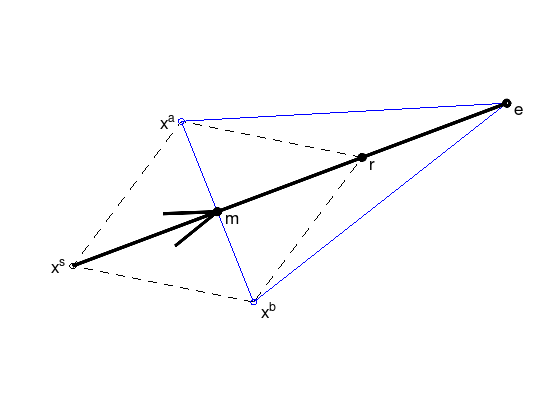
Case 2: Expand

“New point is excellent.”

If \(f(r) < f(x^b)\), compute expanded point

\[ e := m + \beta (m - x^s), \]

with \(\beta > \alpha\), here \(\beta = 2\).

Replace \(x^s\) by \(e\), if \(f(e) < f(r)\), otherwise replace \(x^s\) by \(r\).

function plot_line (points, LineSpec)
  plot (points(:,1), points(:,2), LineSpec{:});
end

function plot_triangle (points, LineSpec)
  % Repeat first point.
  plot_line ([points; points(1,:)], LineSpec);  
end

xb = [ 0.0, 0.0];
xa = [-0.4, 1.0];
xs = [-1.0, 0.2];
m = xb + 0.5 * (xa - xb);
r = m  + 1.0 *  (m - xs);
e = m  + 2.0 *  (m - xs);

points = [xb; xa; xs; m; r; e];
plabel = {'x^b', 'x^a', 'x^s', 'm', 'r', 'e'};

plot_triangle ([xb; xa; xs], {'ko--'});
hold on;
plot_triangle ([xb; xa; r] , {'ko--'});
plot_triangle ([xb; xa; e] , {'bo-'});
quiver (xs(1), xs(2), m(1) - xs(1), m(2) - xs(2), 'ko-', 'LineWidth', 4);
plot_line ([e; r; m], {'ko-', 'LineWidth', 4});

tprops = {'FontSize', 18};
for i = 1:length (plabel)
  if (points(i,1) < -0.3)
    x_offset = -0.12;
    y_offset = 0.0;
  else
    x_offset = 0.04;
    y_offset = -0.04;
  end
  text (points(i,1) + x_offset, points(i,2) + y_offset, plabel{i}, tprops{:});
end

axis equal;
axis off;

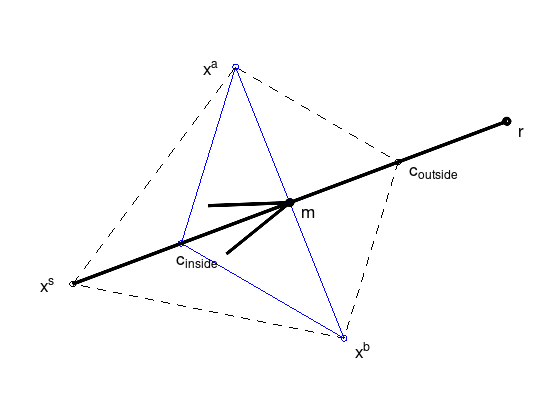
Case 3: Contract / Shrink

“New point is worse.”

If \(f(r) > f(x^a)\), compute a contracting point with \(0 < \gamma < \alpha\), here \(\gamma = 0.5\):

• If \(f(r) > f(x^s)\), contract inside

  \[ c := m - \gamma (m - x^s) \]

• Otherwise contract outside

  \[ c := m + \gamma (m - x^s) \]

Replace \(x^s\) by \(c\), if \(f(c) < f(x^s)\), otherwise shrink (case 4) the whole simplex around \(x^b\):

\[ x^i := \frac{x^i + x^b}{2}, \]

for all \(i = 1, \ldots, n + 1\).

function plot_line (points, LineSpec)
  plot (points(:,1), points(:,2), LineSpec{:});
end

function plot_triangle (points, LineSpec)
  % Repeat first point.
  plot_line ([points; points(1,:)], LineSpec);  
end

xb = [ 0.0, 0.0];
xa = [-0.4, 1.0];
xs = [-1.0, 0.2];
m = xb + 0.5 * (xa - xb);
r =  m + 1.0 *  (m - xs);
co = m + 0.5 *  (m - xs);
ci = m - 0.5 *  (m - xs);

points = [xb; xa; xs; m; r; co; ci];
plabel = {'x^b', 'x^a', 'x^s', 'm', 'r', 'c_{outside}', 'c_{inside}'};

plot_triangle ([xb; xa; xs], {'ko--'});
hold on;
plot_triangle ([xb; xa; co] , {'ko--'});
plot_triangle ([xb; xa; ci] , {'bo-'});
quiver (xs(1), xs(2), m(1) - xs(1), m(2) - xs(2), 'ko-', 'LineWidth', 4);
plot_line ([r; m], {'ko-', 'LineWidth', 4});

tprops = {'FontSize', 18};
for i = 1:length (plabel)
  if (points(i,1) < -0.3)
    x_offset = -0.12;
    y_offset = 0.0;
  else
    x_offset = 0.04;
    y_offset = -0.04;
  end
  if (i == 7)  % c_{inner}
    x_offset = -0.02;
    y_offset = -0.07;
  end
  text (points(i,1) + x_offset, points(i,2) + y_offset, plabel{i}, tprops{:});
end

axis equal;
axis off;

This concludes one step of the simplex method. There is no guarantee for convergence to a local minimum.

Potential stopping criteria are:

• \[ \forall i,j \in \{ 1, \ldots, n + 1 \} \colon\quad \lVert x^i - x^j \rVert \leq \text{TOL}. \]
• \[ \frac{1}{n + 1} \sum _{i = 1}^{n + 1} \left( f(x^i) - f(m) \right)^2 \leq (\text{TOL})^2. \]
• \[ \frac{1}{n + 1} \sum _{i = 1}^{n + 1} \left( f(x^i) - \bar{f} \right)^2 \leq (\text{TOL})^2, \quad \bar{f} := \frac{1}{n + 1} \sum _{i = 1}^{n + 1} f(x^i). \]

Start simplex

Given one vertex \(x^1\) and one edge length \(l\), a regular simplex can be constructed as follows:

• \[ p := \frac{l}{\sqrt{2}} \frac{\sqrt{n + 1} - 1}{n} \]
• \[ q := p (1, \ldots, 1)^{T} \in \mathbb{R}^{n} \]
• \[ x^j := x^1 + q + \frac{l}{\sqrt{2}} e^{j-1}, \quad j = 2, \ldots, n + 1, \]

  where \(e^1, \ldots, e^n\) are the standard unit vectors in \(\mathbb{R}^{n}\).