Unconstrained minimization problems

This section considers the minimization of a function \(f \colon \mathbb{R}^{n} \to \mathbb{R}\) without any constraint functions.

Necessary conditions for a local minimum

Zero slope at a local minimum \(x^{*}\):

\[ \nabla f(x^{*}) = 0 \]

Theorem 2: 1st order optimality condition

Let the open set \(X \subset \mathbb{R}^{n}\) and let \(f \in C^{1}(\mathbb{R}^{n},\mathbb{R})\). If the point \(x^{*} \in X\) is a local minimum of \(f\) over \(X\), then \(\nabla f(x^{*}) = 0\).

Proof:

Let \(d \in \mathbb{R}^{n} \setminus \{0\}\). Because \(X\) is an open set and \(x^{*}\) is a local minimum \(x^{*} + td \in X\), \(x^{*} - td \in X\), \(f(x^{*} + td) - f(x^{*}) \geq 0\), and \(f(x^{*} - td) - f(x^{*}) \geq 0\) hold for sufficiently small \(t > 0\). Because \(f \in C^{1}(\mathbb{R}^{n},\mathbb{R})\) it follows

\[ 0 \leq \lim_{t \to +0} \frac{f(x^{*} + td) - f(x^{*})}{t} = \nabla f(x^{*})^{T}d \]

and

\[ 0 \leq \lim_{t \to +0} \frac{f(x^{*} - td) - f(x^{*})}{t} = -\nabla f(x^{*})^{T}d \]

and it follows \(\nabla f(x^{*}) = 0\).

\[\tag*{$\Box$}\]

Non-negative curvature at a local minimum \(x^{*}\):

\[ \nabla^{2} f(x^{*}) \succeq 0 \quad\text{is positive semi-definite} \]

Theorem 3: 2nd order optimality condition

Let the open set \(X \subset \mathbb{R}^{n}\) and \(f \in C^{2}(\mathbb{R}^{n},\mathbb{R})\). If the point \(x^{*} \in X\) is a local minimum of \(f\) over \(X\), then the Hessian matrix \(\nabla^{2} f(x^{*})\) is positive semi-definite.

Proof:

Let \(d \in \mathbb{R}^{n} \setminus \{0\}\) and \(|t|\) sufficiently small (such that \(x^{*} + td \in X\) for all \(t\) with \(|t| < t_{0}\)).

Using Taylor’s theorem (differentiation with chain-rule) and regarding \(\nabla f(x^{*}) = 0\) gives

\[ f(x^{*} + td) = f(x^{*}) + \frac{1}{2}t^{2}d^{T}\nabla^{2} f(x^{*})d + o(t^{2}). \]

If \(\nabla^{2} f(x^{*})\) was not positive semi-definite, there exists a \(d \in \mathbb{R}^{n} \setminus \{0\}\) with \(d^{T}\nabla^{2} f(x^{*})d < 0\). This is a contradiction for the minimality of \(x^{*}\).

\[\tag*{$\Box$}\]

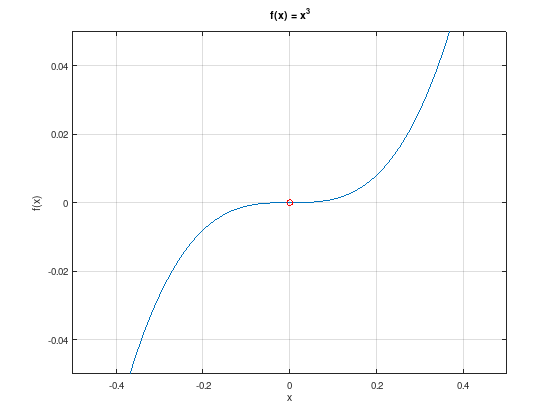
Note

There may exist points that satisfy the necessary 1st and 2nd order conditions but are not local minima. For example:

x = linspace (-0.5, 0.5, 50);
plot (x, x.^3);
hold on;
plot (0, 0, 'ro');
grid on;
xlim ([-0.5, 0.5]);
ylim ([-0.05, 0.05]);
xlabel ('x');
ylabel ('f(x)');
title ('f(x) = x^3');

Sufficient condition for a strict local minimum

Positive curvature at a local minimum \(x^{*}\) (strictly convex):

\[ \nabla^{2} f(x^{*}) \succ 0 \quad\text{is positive definite} \]

Theorem 4: 2nd order sufficient optimality condition

Let \(f \in C^{2}(\mathbb{R}^{n},\mathbb{R})\) and \(x^{*} \in X \subset \mathbb{R}^{n}\) with \(\nabla f(x^{*}) = 0\) and \(\nabla^{2} f(x^{*}) \succ 0\) (positive definite), then \(x^{*}\) is a strict local minimum of \(f\) over \(X\).

Proof:

Application of the Rayleigh–Ritz method, for symmetric matrix \(A \in \mathbb{R}^{n \times n}\) and \(d \in \mathbb{R}^{n} \setminus \{ 0 \}\) there is

\[ \lambda_{\min}(A) \leq \frac{d^{T}Ad}{d^{T}d} \leq \lambda_{\max}(A), \]

where the minimum or maximum is attained for the respective eigenvectors \(d\) of the minimal and maximal eigenvalue.

For a positive definite, symmetric matrix \(A = \nabla^{2} f(x^{*})\) there is \(\lambda := \lambda_{\min}(A) > 0\):

\[ d^{T}\nabla^{2} f(x^{*}) d \geq \lambda \lVert d \rVert_{2}^{2}, \qquad\forall d \in \mathbb{R}^{n}. \]

Applying Taylor’s theorem to \(f\) at \(x^{*}\) (with remainder) gives

\[ f(x^{*} + d) = f(x^{*}) + \nabla f(x^{*})^{T}d + \frac{1}{2}d^{T} \nabla^{2} f(\tilde{x})d \]

with \(\tilde{x} := x^{*} + \theta d\), \(0 < \theta < 1\).

Using \(\nabla f(x^{*}) = 0\) and an expansion:

\[\begin{split} \begin{aligned} f(x^{*} + d) &= f(x^{*}) + \frac{1}{2}\underbrace{d^{T} \nabla^{2} f(x^{*})d}_{\geq \lambda \lVert d \rVert_{2}^{2}} + \frac{1}{2}\underbrace{d^{T} (\nabla^{2} f(\tilde{x}) - \nabla^{2} f(x^{*}))d}_{\text{Cauchy-Schwarz inequality}} \\ &\geq f(x^{*}) + \frac{1}{2} (\lambda - \lVert \nabla^{2} f(\tilde{x}) - \nabla^{2} f(x^{*}) \rVert_{2}) \lVert d \rVert_{2}^{2} \end{aligned} \end{split}\]

Because the Hessian matrix is continuous, there is \(f(x^{*} + d) > f(x^{*})\) for all \(d \neq 0\) with a sufficiently small norm.

\[\tag*{$\Box$}\]

Note

The sufficient condition is not necessary. See for example \(f(x) = x_{1}^{2} + x_{2}^{4}\), where \(x = 0\) is a strict local minimum. However, the Hessian matrix is not positive definite.