UM01

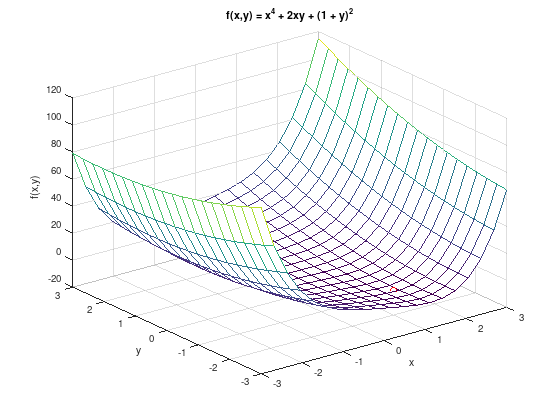
Consider the function \(f(x,y) = x^{4} + 2xy + (1 + y)^{2}\).

1. Create a 3D plot of \(f\) for \(-3 \leq x,y \leq 3\).

f = @(x,y) x.^4 + 2.*x.*y + (1 + y).^2;

[x, y] = meshgrid (linspace (-3, 3, 20));
mesh (x, y, f(x,y));
grid on;
xlabel ('x');
ylabel ('y');
zlabel ('f(x,y)');
title ('f(x,y) = x^4 + 2xy + (1 + y)^2');
hold on;
plot3 (1, -2, -2, 'ro');

2. Compute the gradient \(\nabla f\) and the Hessian matrix \(\nabla^{2} f\).

Solution:

\[\begin{split} \nabla f(x,y) = \begin{pmatrix} \dfrac{\strut\partial}{\strut\partial x} f(x,y) \\ \dfrac{\strut\partial}{\strut\partial y} f(x,y) \end{pmatrix} = \begin{pmatrix} 4x^{3} + 2y \\ 2x + 2(1 + y) \end{pmatrix} \end{split}\]

\[\begin{split} \nabla^{2} f(x,y) = \begin{pmatrix} \dfrac{\strut\partial^{2}}{\strut\partial x\strut\partial x} f(x,y) & \dfrac{\strut\partial^{2}}{\strut\partial x\strut\partial y} f(x,y) \\ \dfrac{\strut\partial^{2}}{\strut\partial y \strut\partial x} f(x,y) & \dfrac{\strut\partial^{2}}{\strut\partial y \strut\partial y} f(x,y) \end{pmatrix} = \begin{pmatrix} 12x^{2} & 2 \\ 2 & 2 \end{pmatrix} \end{split}\]

3. Compute all real stationary points and the respective function values.

Solution:

Stationary points: \(\nabla f = 0\).

\[\begin{split} \begin{aligned} 4x^{3} + 2y &= 0 \\ 2x + 2y + 2 &= 0 \\ \end{aligned} \end{split}\]

From the second equation follows \(y = -(x + 1)\). The resulting equation

\[ 2x^{3} - x - 1 = 0 \]

yields the real stationary point \(P_{1} = (1,-2)^{T}\) with \(f(P_{1}) = -2\).

Use polynomial long division to find more potential real roots:

\[ (2x^{3} - x - 1) : (x - 1) = 2x^{2} + 2x + 1 \]

Finally the equation

\[ x^{2} + x + 0.5 = 0 \]

has only complex roots.

Thus \(P_{1}\) is the only real stationary point.

4. Classify all stationary points.

Solution:

Hessian matrix at \(P_{1}\):

\[\begin{split} \nabla^{2} f(P_{1}) = \begin{pmatrix} 12 & 2 \\ 2 & 2 \end{pmatrix} \end{split}\]

Classification with eigenvalues (roots of the characteristic polynomial):

\[\begin{split} 0 = \det\begin{pmatrix} 12 - \lambda & 2 \\ 2 & 2 - \lambda \end{pmatrix} = (12 - \lambda)(2 - \lambda) - 4 = \lambda^{2} - 14\lambda + 20 \end{split}\]

\[ \Rightarrow \lambda_{1,2} = 7 \pm \sqrt{29} \approx 7 \pm 5.385\ldots > 0 \]

The roots of the characteristic polynomial are all positive. Thus the Hessian matrix is positive definite and \(P_{1}\) is a strict local minimum.

5. Numerical experiments.

Study um01_experiment in Matlab/Octave.