Boosting the Octave hilb function

Created: 2020-07-01

Today, I read an interesting article about Hilbert Matrices in N. Higham’s blog and stumbled over these simple elegant two lines:

function H = hilb_higham (n)
  j = 1:n;
  H = 1 ./ (j' + j - 1);
endfunction

I checked with the implementation of Octave. The currently implemented approach is not as elegant as it can be and includes a for-loop:

function H = hilb_octave (n)
  H = zeros (n);
  tmp = 1:n;
  for i = 1:n
    H(i, :) = 1.0 ./ tmp;
    tmp += 1;
  endfor
endfunction

Fun fact: The “MATLAB implicit expansion feature” mentioned in Higham’s article was introduced in Matlab R2016b. This feature is called broadcasting and was introduced in Octave 3.6.0 back in 2012.

Comparing the implementations clearly shows, that Higham’s solution should be taken.

In the figure generated by the test code below, smaller values are better.

N = 1000;
time_octave_hilb = zeros (1, N);
time_higham_hilb = zeros (1, N);

for i = 1:N
  tic;
  hilb_octave (i);
  time_octave_hilb(i) = toc;
endfor

for i = 1:N
  tic;
  hilb_higham (i);
  time_higham_hilb(i) = toc;
endfor

semilogy (1:N, time_octave_hilb, 'b');
hold on;
semilogy (1:N, time_higham_hilb, 'r');
legend ({"Octave 5.2.0", "Higham"});
xlabel ("Hilbert Matrix Dimension");
ylabel ("Time in seconds");

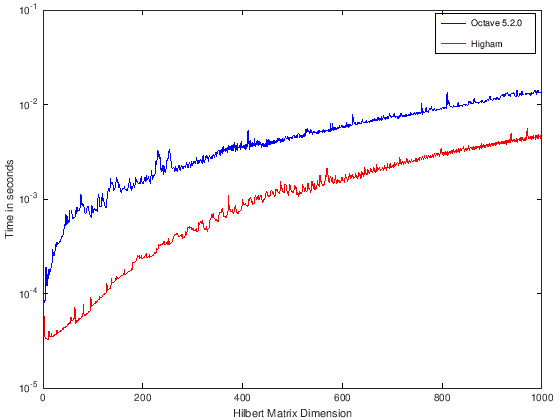
Octave uses Higham’s approach since cset 627da618dcc4.